Research

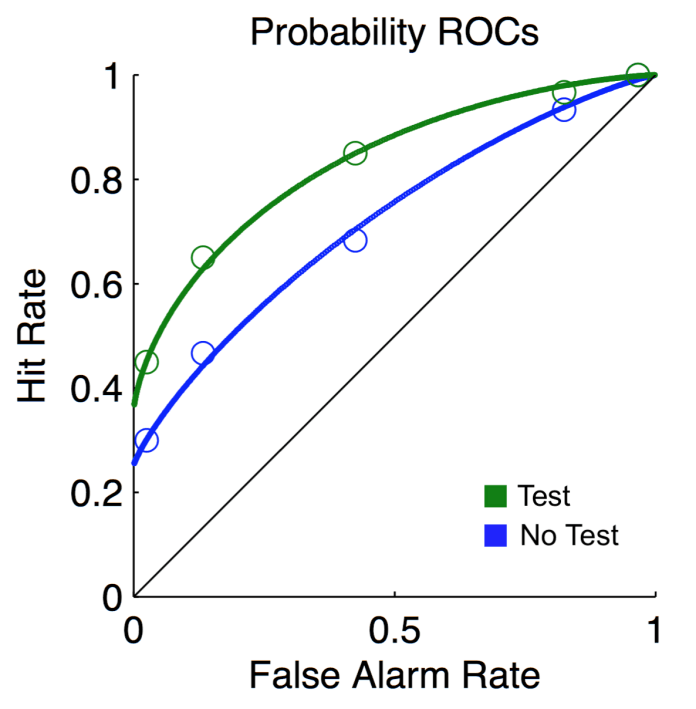
Receiver Operating Characteristic (ROC) curves used to generate recollection and familiarity parameter estimates via the Dual Process Signal Detection model of recognition memory. This plot was created using the ROC Toolbox in MATLAB (Koen et al., 2017; Version 1.1.3).

Exploring the Mechanisms that Underlie the Benefits of Retrieval Practice

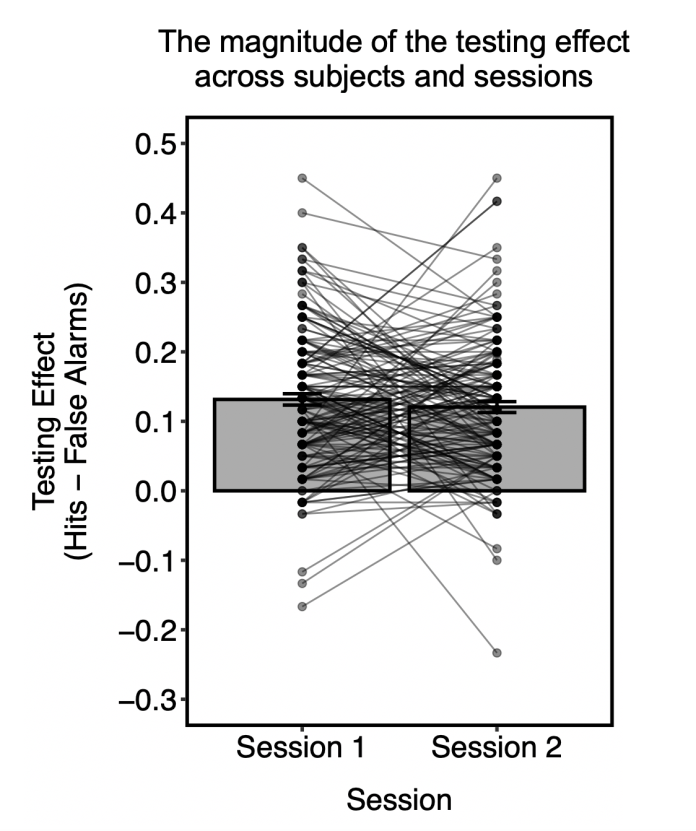
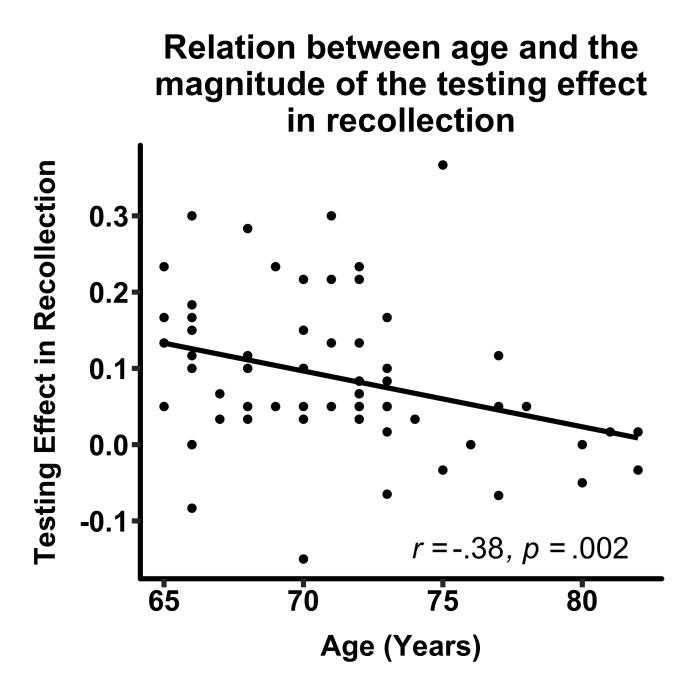
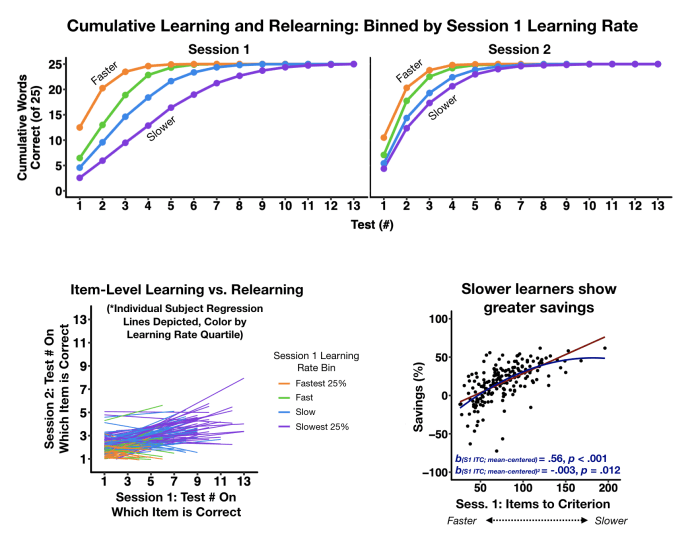
An extensive literature has revealed that taking tests—or retrieval practice—benefits long-term retention of material, a finding referred to as the “testing effect” (Roediger & Karpicke, 2006; Roediger & Butler, 2011; Rowland, 2014; Tulving, 1967). Indeed, retrieving information from memory does not simply serve as a passive indication of what someone knows, but actually serves as a potent means of enhancing long-term memory. Although the robustness of the testing effect is well established, the mechanisms that underlie this benefit of retrieval practice to later memory remain unclear. This research seeks to leverage the Dual-Process Signal-Detection model of recognition memory (Yonelinas, 1994; Jacoby, 1991; Tulving, 1985) to explore the mechanisms that underlie the benefit of retrieval practice.

More on this project:
Publication: Shaffer, R. A. & McDermott, K. B. (2020)
Poster: Shaffer, R. A., Gilmore, A. W., DeSoto, K. A., and McDermott, K. B. (2017)
All experiment data: OSF Link

Mean ± SE for the magnitude of the testing effect per session is depicted in the barplot. Dots indicate the magnitude of the testing effect for each subject, with lines connecting a given subject’s estimate at Sessions 1 and 2. As is apparent in this graph and confirmed with statistical analyses, the testing effect exhibits extremely poor reliability. This plot was created in R.

The Reliability & Stability of the Testing Effect

A small, but growing literature has begun to use an individual differences* approach to explore the testing effect and how it relates to other individual difference factors—obtaining mixed results (e.g., see Brewer & Unsworth, 2012; Pan et al., 2015; Agarwal et al., 2017; Minear et al., 2018; Robey, 2019; Tse et al., 2019; Moreira et al., 2019; Bertilsson et al., 2021, for a few examples). However, the reliability of the testing effect has received little attention, and, to our knowledge, no work has yet examined the test-retest reliability (or stability) of the effect over time. In order to draw meaningful conclusions about potential individual differences in the benefits of testing, it is necessary first to assess the reliability and stability of the testing effect over time. In two experiments, this research aims to address this gap, quantifying both the test-retest and internal consistency reliability of the testing effect.

More on this project:
Manuscript: In preparation
Presentation: Shaffer, R. A. and McDermott, K. B. (November, 2021)

*In individual differences research, the focus moves from estimation of group-level effects to estimation of variability in and the magnitude of effects across subjects, as well as the relation between this variability and other potential individual difference factors (see Goodhew & Edwards, 2019).

Age and the testing effect in recollection

Scatterplot depicting the relation between age and the magnitude of the testing effect in recollection. Increased age predicted decreases in the testing effect in recollection. This plot was created in R.

The Testing Effect and Aging

Despite marked reductions in recollection* with healthy aging (Jennings & Jacoby, 1997; Naveh-Benjamin, 2000; Koen & Yonelinas, 2016), prior work often reveals a benefit of retrieval practice in older adults that is similar in magnitude to that observed in younger adults (Coane, 2013; Meyer & Logan, 2013). This research seeks to address the puzzle of why older adults exhibit such a robust testing effect, despite declines in the very process often considered to be the central contributor to the testing effect. Does retrieval practice for older adults ameliorate existing deficits in recollection or function primarily via preserved familiarity processing? Do the mechanisms that support the benefits of retrieval change with increasing age?

More on this project:
Master's thesis: Shaffer, R. A. (January, 2021)
Publication: In press
Poster: Shaffer, R. A., Balota, D. A., and McDermott, K. B. (Accepted, to be presented in November, 2020)
Sample R scripts for data cleaning, organization, visualization, & analysis: GitHub Link

*Recollection is conceptualized as experiential in nature, consisting of conscious memory for material accompanied by the contextual components of the episode in which the material was experienced (Jacoby, 1991; Yonelinas, 2001, 2002). Under the Dual-Process Signal-Detection model, recollection is conceived of as a threshold process (Parks & Yonelinas, 2007). By contrast, familiarity is conceptualized as an automatic, unconscious form of memory for (or “familiarity” with) material, devoid of the contextual or experiential aspects of the episode. Under the Dual-Process Signal-Detection model, familiarity is conceived of as a signal-detection process.

(Top) Cumulative learning and relearning curves, binned by initial learning rate quartile; (Bottom left) Visualization of within-subject relation between item-level learning and relearning rates; (Bottom right) Relation between initial learning rate and savings in relearning. All plots created in R.

Individual Differences in Relearning from Long-Term Memory

People who learn material more quickly tend to relearn more quickly in a same-day relearning session (Kyllonen and Tirre, 1988) and recall more of the previously-learned material after a delay (e.g., 2 days or 1 week; Zerr et al., 2018). This project expands on this prior work to characterize individual differences in relearning of material from long-term memory. Mixed-effects modeling was used to enable examination of both subject- and item-level learning and relearning rates. Does the relation between learning and relearning rate hold even after accounting for a) item-level learning scores and b) differences in delayed recall? Do faster learners show greater savings in relearning* 1 week later? To address these questions, a drop-out procedure was used in order to equate the degree of initial learning across quicker and slower learners.

More on this project:
Poster: Shaffer, R. A., Spaventa, T., Zerr, C. L., and McDermott, K. B. (November, 2019)

*Although a test of retention may reveal forgetting of all information learned, a relearning session may reveal evidence of preserved memory. Savings in relearning refers to the phenomenon wherein it takes less time to relearn information than it did to learn information the first time. Savings was first experimentally explored by the father of experimental memory research, Hermann Ebbinghaus (1885).

Spring-embedded graph displays the scaled relative strength of relationships between six countries in their collective memories for World War II. Darker, thicker lines indicate greater similarity. Note: This graph shows only relative similarity among the six countries, not the magnitude of any differences in similarity. Spring plot created in R.

How Society Shapes My Memory (And Yours): Collective Memory for World War II

Collective memory within a country consists of “shared” memories that reflect similar interpretations (and even distortions) of the past that typically promote a positive view of the country in question and serve a role in identity formation (Wertsch & Roediger, 2008; Assmann, 2008; Pennebaker & Banasik, 1997). Collective memory’s (sometimes unconscious) influences can be seen everywhere—whether in a simple conversation between two friends or an international peace conference between two distrustful nations. Gaining insight into these collective memories challenges us to see that some of a nation’s most cherished, identity-affirming stories may at times be works of fiction. Further, understanding the mechanisms, whether individually or societally based, by which people learn and remember information is of great importance to addressing many of the challenges we face in our local, national, and global communities.

In exploring these issues, I collaborated with an interdisciplinary team of researchers across multiple universities in the U.S. and internationally (Germany, Japan, and Italy) to examine collective memory for a global event of the past (World War II) in 11 countries (N = 1,338).

More on this project:
Publication: Roediger III, H. L., Abel, M., Umanath, S., Shaffer, R. A., Fairfield, B., Takahashi, M., and Wertsch, J. V. (2019)
Undergraduate Senior Honors Thesis: Shaffer, R. A. (2016)
Dynamic Visualization Code: GitHub Link

Plots depicting timing of fMRI slice acquisition by scanning sequence parameters (ascending vs. interleaved slice acquisition, sparse vs. continuous acquisition, 11 vs. 12 multiband shots).
Slice timing plots created in MATLAB.

Sparse Acquisition Functional Magnetic Resonance Imaging (fMRI) with Multiband Sequences

The aim of this project was to optimize sequence parameters for sparse acquisition* fMRI scanning with multiband** sequences, with the overarching goal of noise reduction in human neuroimaging data. This project began when a pilot fMRI memory experiment I was running required sparse acquisition to allow for subjects to speak aloud their responses in a memory task conducted during the imaging session. Because the use of sparse acquisition with multiband sequences is relatively new, the optimal scanner sequence parameters to reduce slice-by-slice noise had not been determined.

On this project, I worked with an interdisciplinary team of researchers to optimize the scanner sequence parameters for sparse acquisition with multiband sequences. Of particular focus were changes in average slice-by-slice signal intensity as a function of multiband shots (even vs. odd number of shots), slice gap (0%, 10%, 20%, and 30%), repetition time (TR of 3.2s vs. 10s), and acquisition order (interleaved vs. ascending).

More on this project:
Data and analysis scripts: GitHub Link

*In sparse acquisition fMRI scanning, unlike in continuous scanning, there are breaks built into the fMRI pulse sequence in which neuroimaging data is not being collected. Sparse acquisition can be used in order to more readily allow for things like speech in the scanner that can lead to head motion.